PageRank
Update: 对PageRank算法的简单理解 - 知乎 (zhihu.com)
在TextRank之前我们需要先了解一下PageRank算法。事实上它启发了TextRank!PageRank主要用于对在线搜索结果中的网页进行排序。
PageRank对于每个网页页面都给出一个正实数,表示网页的重要程度,PageRank值越高,表示网页越重要,在互联网搜索的排序中越可能被排在前面。
假设整个互联网是一个有向图,节点是网页,每条边是转移概率。网页浏览者在每个页面上依照连接出去的超链接,以等概率跳转到下一个网页,并且在网页上持续不断地进行这样的随机跳转,这个过程形成了一阶马尔科夫链,比如下图:

每个笑脸是一个网页,既有其他网页跳转到该网页,该网页也会跳转到其他网页。在不断地跳转之后,这个马尔科夫链会形成一个平稳分布,而PageRank就是这个平稳分布,每个网页的PageRank值就是平稳概率。
PageRank的核心公式是PageRank值的计算公式。公式如下: 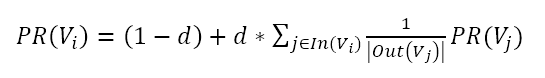
其中,PR(Vi)表示结点Vi的rank值,In(Vi)表示结点Vi的前驱结点集合,Out(Vj)表示结点Vj的后继结点集合。
这个公式来自于《统计学习方法》,等号右边的平滑项(通过某种处理,避免一些突变的畸形值,尽可能接近实际情况)不是(1-d),而是(1-d)/n。
阻尼系数d(damping factor)的意义是,在任意时刻,用户到达某页面后并继续向后浏览的概率。1-d就是用户停止点击,随机跳到新URL的概率。
加平滑项是因为有些网页没有跳出去的链接,那么转移到其他网页的概率将会是0,这样就无法保证存在马尔科夫链的平稳分布。
于是,我们假设网页以等概率(1/n)跳转到任何网页,再按照阻尼系数d,对这个等概率(1/n)与存在链接的网页的转移概率进行线性组合,那么马尔科夫链一定存在平稳分布,一定可以得到网页的PageRank值。
所以PageRank的定义意味着网页浏览者按照以下方式在网上随机游走:以概率d按照存在的超链接随机跳转,以等概率从超链接跳转到下一个页面;或以概率(1-d)进行完全随机跳转,这时以等概率(1/n)跳转到任意网页。
PageRank的计算是一个迭代过程,先假设一个初始的PageRank分布,通过迭代,不断计算所有网页的PageRank值,直到收敛为止,也就是:
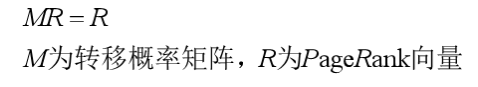
TextRank
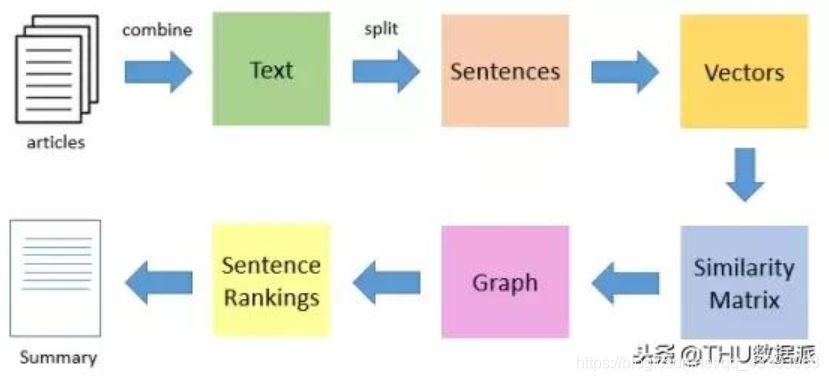
两种算法的相似之处:
- 用句子代替网页
- 任意两个句子的相似性等价于网页转换概率
- 相似性得分存储在一个方形矩阵中,类似于PageRank的矩阵M
不过公式有些小的差别,那就是用句子的相似度类比于网页转移概率,用归一化的句子相似度代替了PageRank中相等的转移概率,这意味着在TextRank中,所有节点的转移概率不会完全相等。

参考文章: