OpenQA论文阅读(四) Open Domain Question Answering Using Early Fusion of Knowledge Bases and Text

论文Open Domain Question Answering Using Early Fusion of Knowledge Bases and Text

论文地址：https://www.aclweb.org/anthology/D18-1455.pdf

论文代码：https://github.com/OceanskySun/GraftNet

​ 知识库问答通常存在一个问题，就是由于知识库不充分导致在一定的推理范围内无法找到相应的答案，因此，可以通过引入额外非结构化文本做辅助增强。本文提出一种开放领域的知识库和文本问答方法。

Abstract

​ 开放领域问题回答(QA)正在从复杂的流水线系统发展到端到端的深度神经网络。专门的神经模型已经被开发出来，用于单独从文本或知识库(KBs)中提取答案。在本文中，我们着眼于一个更实用的设置，即知识库和文本组合的QA，当知识库不完整时，这是合适的。

​ 基于图表示学习的最新进展，用于从包含文本和知识库实体和关系的问题特定子图中提取答案，本文提出了一个新的模型， GRAFT-Net。我们为这个问题构建了一套基准测试任务，它改变了问题的难度、训练数据的数量和知识库的完整性。

问题介绍

​ 在本文中，我们关注的场景是，其中有一个大规模的知识库(Bollacker等人，2008；Auer等人，2007)和一个文本语料库可用，但两者都不足以单独回答所有问题。在问答中，有一些问题可以从文本（Text）中获得答案，有一些问题则可以从知识库（Knowledge Base，KB）中获得答案，因此一个可以想到的问题是，如何将文本和知识库结合起来，因此本文更加关注的场景是，同时使用大规模的知识库和文本进行问答会比单独使用其中一个更加有效。

​ 将文本和知识库结合起来有两种方法，包括：

• late fusion（迟融合）：即分别使用最好的模型对文本和知识库进行问答，然后启发式地将两个答案进行融合。通常这种想法比较简单，且可能会陷入局部最优；
• early fusion（早融合）：即使用单独的模型进行训练，但可以将知识库和文本提前进行结合。这种方法可以灵活地将不同资源结合起来。

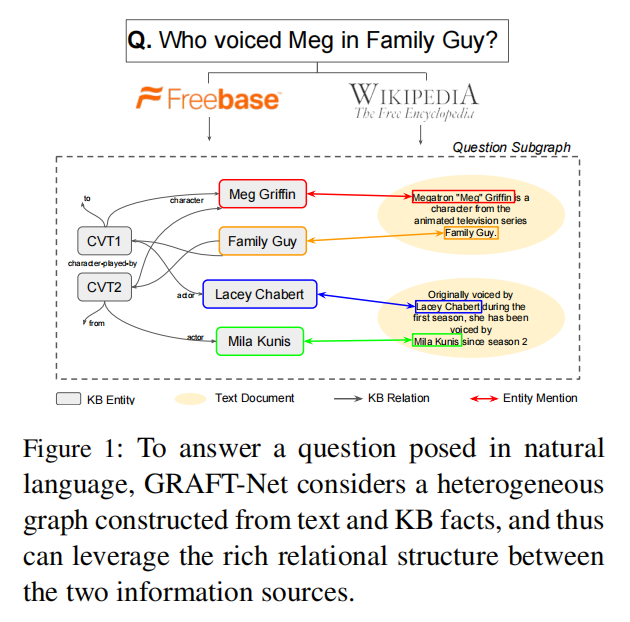
​ 为了实现早期融合，在本文中，我们提出了一种新的基于图卷积的神经网络，称为 GRAFT-Net(Graphs of Relations Among Facts and Text Networks)，

​ 首先，我们提出了异构更新规则，它处理的KB节点不同于文本节点：例如，基于LSTM的更新用于将信息传播到和离开文本节点（3.2）。其次，我们引入了一种定向传播方法，该方法的灵感来自于IR中的个性化Pagerank(Haveliwala，2002)，该方法限制了嵌入在图中的传播，以遵循从与该问题（3.3）链接的种子节点开始的路径。根据经验，我们证明了这两个扩展对于QA的任务都是至关重要的。

方法

​ 任务描述：给定一个问句和对应的主题词（种子实体），根据主题词获得对应的子图，以及实体与文档链接后构成异构图，对异构图中的每个实体以及文档内的名词进行二分类，选择超过阈值的实体或名词。

​ 因此本文将KBQA视为对图中各个实体结点的二分类问题。

概览

定义问句 $q$以及其对应的所有答案$\{a\}_q$，因此对于问句$q$对应的子图$\mathcal{V}_q$ 中的各个实体 $v\in\mathcal{V}_q$，其标签满足（1）当$v\in\{a\}_q$时，$y_v=1$否则（2）当$v\in(\mathcal{V}_q - \{a\}_q)$时，$y_v=0$。因此可以将本任务视为对每个结点的二分类，在传统的图表征任务中，结点表征通常为“聚集-应用-发散”的过程，即先将周围的实体的信息聚集在某个实体上使得该实体能够拥有周围实体的信息并进行相应的迭代计算，其次通过梯度向外扩散。

传统的图表征公式可表示为：

$$h_v^{l} = \phi(h_v^{l-1},\sum_{v'\in N_r(v)}h_{v'}^{l-1})$$

其中 $N_r(v)$ 表示实体$v$的关于关系边$r$ 的邻接实体，$\phi$则为前馈神经网络。

不同于传统的图表征方法，本文不同点在于：（1）我们的图包含异构结点、（2）我们希望在迭代训练时是基于问句进行的。

结点初始化

​ 实体初始化：定义每个实体的向量为$x_v$，其可以使用知识表示学习（Knowledge Base Embedding）进行预训练。网络结点初始化则表示为$h_v^{(0)} = x_v$。

​ 文档初始化：对于文档结点，需要对整个文档进行表示，因此定义$H_d^{(l)}\in\mathcal{R}^{|d|\times n}$表示第 $l$次迭代时文档的表征向量，初始化可使用一层长短期记忆神经网络：

$$H_d^{(0)} = LSTM(w_1,w_2,...)$$

为了便于表示，我们定义$H_{d,p}^{(l)}$表示第$ l$次迭代计算时，文档 $d$ 的第$ p$个单词（token）的输出表征向量。

异构更新

网络中包含原有的实体结点以及链接的文档结点，如何表示异构图是图表征任务中的一个研究点，本文希望能够充分学习到异构图中的信息。

​ 实体表征：

​ 在第$l$轮迭代更新时，实体结点表征$H_{d,p}^{(l)}$可综合为如下公式，从上往下其包含四个部分信息：

h_v^{(l)} = \text{FFN}\left( \begin{bmatrix} h_v^{(l-1)} \\ h_q^{(l-1)} \\ \sum_r \sum_{v'\in N_r(v)} \alpha_{r}^{v'} \psi_r(h_{v'}^{(l-1)}) \\ \sum_{(d,p) \in M(v)} H_{d,p}^{(l-1)} \end{bmatrix} \right). \label{eq:entity-upd}

（1）来自于上一迭代时计算得到的实体表征$h_v^{(l-1)}$ ；
（2）来自于上一迭代时计算得到的问句表征$h_q^{(l-1)}$；
（3）来自当前实体 $v$有关所有关系 $r$的邻接实体的表征信息$h_{v'}^{(l-1)}$，值得注意的是，其实两个求和，外层的求和表示对所有该实体所相连边的关系，内层的求和表示在某一关系下所有的相邻的实体，权重$\alpha_r^{v'}$则表示邻接的实体与当前实体的权重，$\psi_r$表示线性函数，定义为:

---

参考资料

1. 《利用知识库和文本结合来改进开放域QA》阅读笔记 - 知乎 (zhihu.com)

2. 论文解读：Open Domain Question Answering Using Early Fusion of Knowledge Bases and Text_夏栀的博客-CSDN博客